这篇博客对以下问题进行粗略的讨论：

• 最小二乘法和高斯分布的联系
• 高斯牛顿法与联合高斯分布的信息矩阵、信息向量的关系
• 舒尔补进行边缘化，边缘化产生了先验，为啥舒尔补这么随处可见
• 卡尔曼滤波（KF）、扩展KF（EKF）、迭代EKF（IEKF）、滑动窗口滤波（SWF）、光束平差法（bundle adjustment），它们的关系
• 优化问题中的first estimate Jacobian（FEJ）

乘法原理和贝叶斯公式

一个联合概率密度函数可以写成连乘的形式；其中$\bf {x_i}$也可以是个向量：

$$p(x_1,x_2,\dots) = p(x_1)p(x_2|x_1)p(x_3|x_1,x_2)\dots$$

如果只有两个（两组）随机变量，联合概率密度函数可以写成两种形式：

$$\begin{aligned} p(x,y) &= p(x)p(y|x) \\ &= p(y)p(x|y) \end{aligned}$$

调整一下就是常见的贝叶斯公式：

$$p(x|y) = \frac{p(y|x)p(x)}{p(y)}$$

赋予它一些含义：$p(x|y)\propto p(y|x)p(x)=p(x,y)$称为后验(posterior)，$p(y|x)$称为似然(likelihood)，$p(x)$称为先验(prior)。

将系统建模为以下两个方程：运动方程和观测方程：

$$\begin{aligned} \begin{cases} \bf x_k &= \bf f(x_{k-1}, \overbrace{w_k}^\text{输入}, \overbrace{u_k}^\text{噪声}) \\ \bf y_k &= \bf g(x_{k}, \underbrace{v_k}_\text{噪声}) \end{cases} \end{aligned}$$

我们要估计的状态量是$\bf x$，而传感器对$\bf x$测量产生了$\bf y$。如果知道了$\bf x_{k-1}$的（后验）分布$\bf p(\hat x_{k-1}) = p(x_{k-1}|y_{k-1})$，那么我们可以通过运动方程估计$\bf x_{k}$的（先验）分布$\bf p(\check x_{k})$；也就是说运动方程将$\bf x_{k-1}$的后验传递到$\bf x_{k}$产生了先验。在$\bf x_{k}$处通过观测方程观测到$\bf y_k$，描述的是$\bf p(y_k|x_k)$这样一个似然概率。通过先验和似然，求得这时刻的后验概率$\bf p(\hat x_{k}) = p(x_{k}|y_{k})$。

如果我们没有运动方程而只有观测方程，也就是bundle adjustment中常见的情况，那么可以说先验是一个方差无穷大的分布，那么最大化后验概率等价于最大似然；如果通过一些方法估计了先验，比如说滑动窗口过去时刻的状态估计可以对窗口内的估计值产生先验，或者说有了一个运动方程，那么最大化后验的话就是最大化似然和先验的乘积；如果连传感器测量值也是有先验的，那么就是全贝叶斯估计了。

最小二乘法

首先重温一下二次型。有n个变量$\bf{x} = \begin{bmatrix} x_i \end{bmatrix}_n$，它们两两相乘并求和，每个乘积都有一个权重$a_{ij}$，可以表达为：

$$\begin{aligned} sum &= \sum_{i=1}^{n} \sum_{j=1}^{n} a_{ij}x_ix_j \\ &= \bf{x}^TA\bf{x} \end{aligned}$$

其中$\bf{A} = \begin{bmatrix} a_{ij} \end{bmatrix}_{n*n}$。考虑到乘法和加法具有交换律，即$x_ix_j = x_jx_i$，同项可以合并，则取$a_{ij} = a_{ji}$，使得$\bf{A}$是一个对称方阵。则一个二次型对应有且只有一个对称方阵，一个对称方阵也可对应一个二次型。

二次型的和还是二次型，即$\bf{x}^TA\bf{x} + \bf{x}^TB\bf{x} = \bf{x}^T(A+B)\bf{x}$。

联合高斯分布的概率密度函数(PDF)如下：

$$\mathcal N(\bf\mu, \bf\Sigma) \sim p(\bf x) = \frac{1}{\sqrt{(2\pi)^Ndet(\bf\Sigma)}}exp\left(-\frac{1}{2}(\bf x - \bf\mu)^T\Sigma^{-1}(\bf x - \bf\mu)\right)$$

其中$\bf\mu = \begin{bmatrix} \mu_1&…&\mu_N \end{bmatrix}^T$ 为N个随机变量的均值，$\bf\Sigma = E\left[(x - \mu)(x - \mu)^T\right]$为N个随机变量的协方差矩阵。可以看出指数部分是一个二次型。

我们仅考虑如何由观测方程估计状态值。假设受高斯噪声影响的传感器读出的测量值符合高斯分布，其协方差矩阵为$\bf{W}$，而且由状态变量$\bf{x}$到测量值$\bf{y}$的模型线性的。我们把$\bf y$的概率密度函数建模为$\bf x$的条件概率：

$$\begin {aligned} \bf{y} &= \bf{C}\bf{x} + \bf{w} \\ \bf p(y|x) &\sim \mathcal N(\bf{C}\bf{x}, W) \\ &= \eta *\bf exp\Bigl(- \frac{1}{2} (y-Cx)^TW^{-1}(y-Cx)\Bigr) \end {aligned}$$

我们不能完全相信传感器读到的值$\bf{y}$，而要求$\bf{y}$分布的最大值$\bf \hat{y} = C\hat{x}$，才能得到状态值的最佳估计$\bf \hat{x}$。那么我们就要最大化$\mathcal N(\bf{C}\bf{x}, W)$，即最小化指数中的二次型：

$$\begin{aligned} \bf x &= \arg \min_x \Bigl((\underbrace{\bf y-Cx}_\text{误差函数e})^T\bf W^{-1}(y-Cx)\Bigr) \\ &= \arg \min_x (\bf \underbrace{e^TW^{-1}e}_\text{目标函数f}) \end{aligned}$$

如果假设$\bf y$中每一项都是对$\bf x$的一次观测，或者说$n$维的$\bf x$经过了$m$次观测得到$m$维的$\bf y$，那么现在要从$m$维的$\bf y$恢复出$n$维的$\bf x$最有可能的值。我们令目标函数对$\bf x$的导数为0

$$\begin{aligned} \bf \frac{\partial f}{\partial x} &= 0 \\ &= \frac{\partial }{\partial \bf x} \Bigl( \bf (y-Cx)^TW^{-1}(y-Cx) \Bigr) \\ &= \frac{\partial }{\partial \bf x} \Bigl( \bf (C^{-1}y-x)^T\underbrace{C^TW^{-1}C}_\text{将C提出来}(C^{-1}y-x) \Bigr) \\ 0&= 2\bf C^TW^{-1}C(C^{-1}y-x) \\ \bf C^TW^{-1}Cx &= \bf C^TW^{-1}y \end{aligned}$$

最后得到熟悉的批量最小二乘法的求解公式。如果观测是独立同分布的，不妨设协方差$\bf W = \sigma I$，约去$\sigma$得到$\bf C^TCx = \bf C^Ty$就是常见的最小二乘法了。如果每次观测是独立但是分布都不同，则$\bf W^{-1}$还是一个对角矩阵，扮演了权重的角色。

非线性优化

上文中我们把观测方程假设为线性的，但是现实中几乎不存在与状态栏成线性关系的观测方程，例如三角定位：状态量是标签的坐标，而测量的是标签与多个基站之间的距离；xyz坐标跟距离显然不是线性关系。

假设$\bf y$满足正态分布，经过非线性变换之后的$\bf x$的概率密度函数，虽然有可能是单峰的钟形的，并不一定是对称的，意味着极大值并不一定是均值（期望）；我们一般使用最大似然法估计的是概率密度函数的极大值，而我们通常评价一个估计方法是否无偏考虑的是它的期望，因此这时候最大似然或者最大后验这种估计最值的方法是“有偏”的。虽然如此，这并不能说非线性条件下就不能用最大似然法，要知道这仅仅是一个评价指标上的取舍。

我们不妨假设$\bf y$满足正态分布，毕竟传感器的噪声“就是”高斯的。状态方程是非线性方程，但可以通过一阶泰勒展开将其线性化。我们将其写成迭代的形式：

$$\begin{aligned} \bf{y} &= \bf{g}(\bf{x_i}) + \bf{w} \\ & \approx \bf \underbrace{g(x_{i-1})}_\text{估计观测值} + \underbrace{J}_\text{雅可比}*\underbrace{(x_i-x_{i-1})}_{\bf \Delta x_i} + w \\ \Bigl(& \text{令}\bf \hat y_i = g(x_{i-1})\Bigr) \\ & \sim \mathcal N(\bf \hat y_i + J\Delta x_i, W) \\ &= \eta *\bf exp\Bigl(- \frac{1}{2} (\underbrace{y-\hat y_i}_{\bf e_i} - J\Delta x_i)^TW^{-1}(y-\hat y_i - J\Delta x_i)\Bigr) \\ &= \eta *\bf exp\Bigl(- \frac{1}{2} (e_i - J\Delta x_i)^TW^{-1}(e_i - J\Delta x_i)\Bigr) \end{aligned}$$

于是目标函数变为$\bf (e_i - J\Delta x_i)^TW^{-1}(e_i - J\Delta x_i)$，自变量变为了$\bf\Delta x_i$。套用上文的方法，对$\bf\Delta x_i$求导等于0，得到

$$\begin{aligned} \bf \underbrace{J^TW^{-1}J}_{\text{海森矩阵}H}\Delta x &= \bf \underbrace{J^TW^{-1}e_i}_{b}\\ \bf Hx &= \bf b \end{aligned}$$

这就是高斯牛顿法。每一步迭代都算得一个$\bf\Delta x_i$，进而更新$\bf x_i$。高翔十四讲中将误差函数$\bf e = y-g(x)$展开为$\bf e + J\Delta x$，而上文是将$\bf g(x)$展开的，因此雅可比矩阵有个负号的不同；十四讲中直接给出的目标函数没有$\bf W$，相当于假设$\bf W = \sigma I$，即$\bf y$的每一项都独立同分布从而约去了。

高斯分布的信息矩阵

联合高斯分布除了可以表达为均值和协方差矩阵形式以外，还可以表达为信息矩阵和信息向量的形式。后两者在《概率机器人》中被称为“正则参数”，这两种形式是对偶的：

$$\begin{aligned} \bf\mathcal N(\mu, \Sigma) \begin{cases} \bf \Sigma &= \bf \Omega^{-1} \\ \bf \mu &= \bf \Omega^{-1} \xi \end{cases}, \qquad \bf\mathcal N^{-1}(\xi, \Omega) \begin{cases} \bf \Omega &= \bf \Sigma^{-1} \\ \bf \xi &= \bf \Sigma^{-1} \mu \end{cases} \end{aligned}$$ $$\bf \eta exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)) \qquad \eta'exp(-\frac{1}{2}x^T\Omega x + x^T\xi)$$

之所以考虑用信息矩阵表示，是因为高斯分布的指数项的二次型矩阵是协方差矩阵的逆，于是可以表达得更简单。之所以叫“信息”矩阵，就是因为它是概率密度函数的对数项，而熵就是概率的负对数。对于任意一个概率密度函数，用高斯去近似它，那么求其对数并展开为二次型就可以得到信息矩阵和信息向量；但是并不是所有时候这个信息矩阵都是可以求逆得到协方差矩阵的，这时候这个“高斯分布”只能以信息矩阵的形式存下来。如果说卡尔曼滤波针对的是协方差矩阵，那么相对应也有所谓“信息滤波”针对信息矩阵，二者形式上十分对称。

我们将估计量建模为期望$\theta$，将测量值建模为随机变量$\bf x$，于是得到条件概率$\bf p(x|\theta)$。我们觉得它应该是个正态分布，虽然不一定是，但是可以近似，于是我们想或许对它对数值作泰勒展开即可。费歇尔信息矩阵（Fisher information matrix）也有相似的定义，虽然它本意可能不是为了“近似”高斯分布：

$$\begin{aligned} \bf \mathcal I(\theta) &= \bf E\Bigl[ \Bigl( \frac{\partial \log p(x|\theta)}{\partial \theta} \Bigr)\Bigl( \frac{\partial \log p(x|\theta)}{\partial \theta} \Bigr)^T \Bigr] \\ \text{某些情况下} &= \bf-E\Bigl[ \frac{\partial^2\log p(x|\theta)}{\partial \theta^2} \Bigr] \end{aligned}$$

注意式子中的期望。如果$\bf p(x|\theta)$真的是高斯的那么两个式子相等，都等于协方差矩阵的逆，也即是“那个”信息矩阵。

$$\begin{aligned} \bf p(x|\theta) &\sim \bf \mathcal N(\theta, \Sigma) \\ \bf \frac{\partial \log p(x|\theta)}{\partial \theta} &= \bf \Sigma^{-1}(x - \theta) \\ \bf \frac{\partial^2\log p(x|\theta)}{\partial \theta^2} &= \bf -\Sigma^{-1} \\ \bf -E\Bigl[ \frac{\partial^2\log p(x|\theta)}{\partial \theta^2} \Bigr] &= \bf \Sigma^{-1} \\ \bf E\Bigl[ \Bigl( \frac{\partial \log p(x|\theta)}{\partial \theta} \Bigr)\Bigl( \frac{\partial \log p(x|\theta)}{\partial \theta} \Bigr)^T \Bigr] &= \bf E\bigl[ \Sigma^{-1}(x - \theta)(x - \theta)^T\Sigma^{-1} \bigr] \\ &= \bf \Sigma^{-1}E\Bigl[(x - \theta)(x - \theta)^T\Bigr]\Sigma^{-1} \\ &= \bf \Sigma^{-1}\Sigma\Sigma^{-1} \\ &= \bf \Sigma^{-1} \\ \end{aligned}$$

Fisher信息矩阵的逆被称为克拉美罗下界（CRLB），任意对$\theta$的估计方法得到结果的协方差都要大于CRLB，如果它达到了CRLB，那么它估计的状态的方差最小，是“最优”的。感性的认识：很多“最x值”都会牵涉到高斯分布，比如说在给定方差下正态分布使得熵最大，因此信源功率有限的情况下，信道容量（即互信息的最大值）在信源是高斯分布的情况下达到。同样道理如果估计量的分布真的是高斯的，那么就能得到“最优”估计。

我们回过头来看信息矩阵和信息向量。如果测量值$\bf y$与待估计的状态值$\bf x$是线性的，那么得到分布如下：

$$\begin{aligned} \bf{y} &= \bf{C}\bf{x} + \bf{w} \\ \bf p(y|x) &\sim \mathcal N(\bf{C}\bf{x}, W) \\ &= \eta *\bf exp\Bigl(- \frac{1}{2} (y-Cx)^TW^{-1}(y-Cx)\Bigr) \\ &= \eta *\bf exp\Bigl(- \frac{1}{2} \bf (C^{-1}y-x)^T\underbrace{C^TW^{-1}C}_\text{将C提出来}(C^{-1}y-x) \Bigr) \\ & \Downarrow \text{（因为我们只考虑观测方程，没有先验）} \\ \bf p(x|y) &\sim \bf \mathcal N(C^{-1}y,\quad (C^TW^{-1}C)^{-1}) \\ \text{（写成信息形式）} &= \bf \mathcal N^{-1}(C^TW^{-1}y,\quad C^TW^{-1}C) \end{aligned}$$

我们没有$\bf x,y$的先验，这其实是最大似然法。我们构建了最小二乘方程如下：

$$\begin{aligned} \bf \underbrace{C^TW^{-1}C}_\text{信息矩阵}x &= \bf \underbrace{C^TW^{-1}y}_\text{信息向量} \end{aligned}$$

如果是非线性的，那么我们进行一阶泰勒展开以线性化：

$$\begin{aligned} \bf{y} &= \bf{g}(\bf{x_i}) + \bf{w} \\ & \approx \bf g(x_{i-1}) + J(x_i-x_{i-1}) + w \\ \Bigl(& \text{令}\bf \hat y_i = g(x_{i-1})\Bigr) \\ \bf p(y|x_i) & \sim \bf \mathcal N(\hat y_i + J\Delta x_i, W) \\ &= \eta *\bf exp\Bigl(- \frac{1}{2} (\underbrace{y-\hat y_i}_{\bf e_i} - J\Delta x_i)^TW^{-1}(y-\hat y_i - J\Delta x_i)\Bigr) \\ &= \eta *\bf exp\Bigl(- \frac{1}{2} (e_i - J\Delta x_i)^TW^{-1}(e_i - J\Delta x_i)\Bigr) \\ &= \eta *\bf exp\Bigl(- \frac{1}{2} (J^{-1}e_i - \Delta x_i)^TJ^TW^{-1}J(J^{-1}e_i - \Delta x_i) \Bigr) \\ & \Downarrow \text{（还是因为我们只考虑观测方程，没有先验）} \\ \bf p(\Delta x_i|e_i) &\sim \bf \mathcal N (J^{-1}e_i, \quad (J^TW^{-1}J)^{-1}) \\ \text{（写成信息形式）} &= \bf \mathcal N^{-1} (J^TW^{-1}e_i, \quad J^TW^{-1}J) \end{aligned}$$

得到的高斯牛顿法的求解方程是:

$$\begin{aligned} \bf \underbrace{J^TW^{-1}J}_{\text{海森矩阵}H}\Delta x &= \bf \underbrace{J^TW^{-1}e_i}_{b}\\ \bf Hx &= \bf b \end{aligned}$$

从而可以看出，原来高斯牛顿法中的海森（Hessian）矩阵就是信息矩阵！等式右边的向量就是信息向量！ 也有一种说法是“高斯牛顿法定义了费歇尔信息矩阵”。

舒尔补进行边缘化

边缘化指的是以下过程：假设一个联合分布为$p(x_1,x_2, \dots, x_i, x_{i+1}, \dots)$，现在我们要将随机变量的维度降到$i$维，那么就要将$i+1$之后的变量扔掉，剩下了联合分布$p(x_1,x_2, \dots, x_i)$，也就是“边缘化”（marginalization）。

如果我们以均值和协方差矩阵的方式来表示联合分布，那么边缘化就很直接：把对应的均值和协方差矩阵部分抠掉就行了。

$$\begin{aligned} \bf p(x, y) &= \mathcal N \left( \begin{bmatrix} \mu_x \\ \mu_y \end{bmatrix}, \begin{bmatrix} \bf\Sigma_{xx}&\bf\Sigma_{xy}\\\bf\Sigma_{yx}&\bf\Sigma_{yy} \end{bmatrix} \right) \\ \Downarrow \\ \bf p(x) &= \bf \mathcal N(\mu_x, \Sigma_{xx}) \\ \end{aligned}$$

但是如果以信息向量和信息矩阵来表示联合分布的话，就不能直接将对应部分的信息矩阵和信息向量抠掉了，边缘化需要用到舒尔补。如果直接抠掉的话就求的是条件分布了，下面会给予证明。 相对应地，对原来的协方差矩阵使用舒尔补的方法就反而得到条件分布，可见这两种表达形式的对偶性。

舒尔补与矩阵求逆引理

Schur complement将一个分4块的可逆矩阵分解为上三角×对角×下三角(UDL)，或者下三角×对角×上三角(LDU)形式：

$$\begin{aligned} \begin{bmatrix} \bf A&\bf B\\\bf C&\bf D \end{bmatrix} &= \begin{bmatrix} \bf I& \\ \bf CA^{-1}&\bf I \end{bmatrix} \begin{bmatrix} \bf A& \\ &\bf D-CA^{-1}B \end{bmatrix} \begin{bmatrix} \bf I&\bf A^{-1}B \\ &\bf I \end{bmatrix} \\ &= \begin{bmatrix} \bf I&\bf BD^{-1} \\ &\bf I \end{bmatrix} \begin{bmatrix} \bf A-BD^{-1}C& \\ &\bf D \end{bmatrix} \begin{bmatrix} \bf I& \\ \bf D^{-1}C&\bf I \end{bmatrix} \end{aligned}$$

其中$\bf D-CA^{-1}B$和$\bf A-BD^{-1}C$就是舒尔补，字母顺序是顺时针的，方便记忆。

求逆也很方便：

$$\begin{aligned} \begin{bmatrix} \bf A&\bf B\\\bf C&\bf D \end{bmatrix}^{-1} &= \begin{bmatrix} \bf I&\bf -A^{-1}B \\ &\bf I \end{bmatrix} \begin{bmatrix} \bf A^{-1}& \\ &\bf (D-CA^{-1}B)^{-1} \end{bmatrix} \begin{bmatrix} \bf I& \\ \bf -CA^{-1}&\bf I \end{bmatrix} \\ &= \begin{bmatrix} \bf I& \\ \bf -D^{-1}C&\bf I \end{bmatrix} \begin{bmatrix} \bf (A-BD^{-1}C)^{-1}& \\ &\bf D^{-1} \end{bmatrix} \begin{bmatrix} \bf I&\bf -BD^{-1} \\ &\bf I \end{bmatrix} \end{aligned}$$

乘起来，得到等价的矩阵求逆的等式。这些等式被称为矩阵求逆引理或者SMW等式：

$$\begin{aligned} \begin{bmatrix} \bf A&\bf B\\\bf C&\bf D \end{bmatrix}^{-1} &= \begin{bmatrix} \bf A^{-1}+A^{-1}B(D-CA^{-1}B)^{-1}CA^{-1} & \bf -A^{-1}B(D-CA^{-1}B)^{-1} \\ \bf -(D-CA^{-1}B)^{-1}CA^{-1} & \bf (D-CA^{-1}B)^{-1} \end{bmatrix} \\ &= \begin{bmatrix} \bf (A-BD^{-1}C)^{-1} & \bf -(A-BD^{-1}C)^{-1}BD^{-1} \\ \bf -D^{-1}C(A-BD^{-1}C)^{-1} & \bf D^{-1}+D^{-1}C(A-BD^{-1}C)^{-1}BD^{-1} \end{bmatrix} \end{aligned}$$

舒尔补可以在高斯消元法解线性方程组的时候凑出来：

$$\begin{aligned} &\begin{bmatrix} \bf A&\bf B\\\bf C&\bf D \end{bmatrix} \begin{bmatrix} \bf x_1\\\bf x_2 \end{bmatrix} = \begin{bmatrix} \bf b_1\\\bf b_2 \end{bmatrix} \\ & \qquad\qquad \Downarrow \\ &\begin{cases} \bf Ax_1 + Bx_2 = b_1 \\ \bf Cx_1 + Dx_2 = b_2 \end{cases} \text{（用下式消去上式）} \begin{cases} \bf (A-BD^{-1}C)x_1 = b_1 - BD^{-1}b_2 \\ \bf Dx_2 = b_2 + Cx_1 \end{cases} \\ & \qquad\qquad \Downarrow \\ & \begin{bmatrix} \bf A-BD^{-1}C& \\ &\bf D \end{bmatrix} \begin{bmatrix} \bf x_1\\\bf x_2 \end{bmatrix} = \begin{bmatrix} \bf b_1 - BD^{-1}b_2\\\bf b_2 + Cx_1 \end{bmatrix} \end{aligned}$$

可见现在参数矩阵中出现了$\bf D$关于$\bf A$的舒尔补。同理如果用上式消去下式，就会出现$\bf A$关于$\bf D$的舒尔补。剩下的两个三角矩阵要凑出来也并不难。

联合高斯分布（正则参数）的边缘化

我们考虑使用信息矩阵和信息向量：

$$\begin{aligned} p(\bf x) &= \bf\mathcal N^{-1}(\xi_x, \Omega_{xx}) \\ p(\bf y) &= \bf\mathcal N^{-1}(\xi_y, \Omega_{yy}) \\ p(\bf x, y) &= \bf\mathcal N^{-1} \left( \begin{bmatrix} \xi_x \\ \xi_y \end{bmatrix}, \begin{bmatrix} \bf\Omega_{xx}&\bf\Omega_{xy}\\\bf\Omega_{yx}&\bf\Omega_{yy} \end{bmatrix} \right) \\ &= \bf \eta' exp \left( -\frac{1}{2}\begin{bmatrix} \bf x \\ \bf y \end{bmatrix}^T \begin{bmatrix} \bf\Omega_{xx}&\bf\Omega_{xy}\\\bf\Omega_{yx}&\bf\Omega_{yy} \end{bmatrix} \begin{bmatrix} \bf x \\ \bf y \end{bmatrix} + \begin{bmatrix} \bf x \\ \bf y \end{bmatrix}^T\begin{bmatrix} \xi_x \\ \xi_y \end{bmatrix} \right) \end{aligned}$$

再根据上文矩阵求逆引理，当使用信息矩阵和信息向量来表达联合分布时候，虽然$\bf \Omega = \Sigma^{-1}$，但是分块的话$\bf \Omega_{xx} \neq \Sigma_{xx}^{-1}$，$\bf \Omega_{yy} \neq \Sigma_{yy}^{-1}$。

然而，$\bf \Omega_{xx} = \left( \Sigma_{xx} - \Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx} \right)^{-1}$，恰好是$\bf p(x|y)$条件分布的信息矩阵！条件分布求法如下：

$$\begin{aligned} &\overbrace{ \begin{bmatrix} \bf x-\mu_x \\ \bf y-\mu_y \end{bmatrix}^T \underbrace{\begin{bmatrix} \bf\Sigma_{xx}&\bf\Sigma_{xy}\\\bf\Sigma_{yx}&\bf\Sigma_{yy} \end{bmatrix}^{-1}}_\text{使用求逆的舒尔补展开} \begin{bmatrix} \bf x-\mu_x \\ \bf y-\mu_y \end{bmatrix} }^{\bf p(x,y)\text{联合概率密度}} \\ =&\underbrace{ \begin{bmatrix} \bf x-\mu_x \\ \bf y-\mu_y \end{bmatrix}^T \begin{bmatrix} I & \\ \bf-\Sigma_{yy}^{-1}\Sigma_{yx} & I \end{bmatrix} } \begin{bmatrix} \bf(\Sigma_{xx} - \Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx})^{-1} & \\ & \bf\Sigma_{yy}^{-1} \end{bmatrix} \underbrace{\begin{bmatrix} I & \bf-\Sigma_{xy}\Sigma_{yy}^{-1} \\ & I \end{bmatrix} \begin{bmatrix} \bf x-\mu_x \\ \bf y-\mu_y \end{bmatrix}} \\ =& \begin{bmatrix} \bf x-\mu_x-\Sigma_{xy}\Sigma_{yy}^{-1}(y-\mu_y) \\ \bf (y-\mu_y) \end{bmatrix} ^T \underbrace {\begin{bmatrix} \bf(\Sigma_{xx} - \Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx})^{-1} & \\ & \bf\Sigma_{yy}^{-1} \end{bmatrix} }_\text{对角块矩阵，二次型展开很方便} \begin{bmatrix} \bf x-\mu_x-\Sigma_{xy}\Sigma_{yy}^{-1}(y-\mu_y) \\ \bf (y-\mu_y) \end{bmatrix} \\ =& \underbrace{ \bf (x-\mu_x-\Sigma_{xy}\Sigma_{yy}^{-1}(y-\mu_y))^T(\Sigma_{xx} - \Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx})^{-1}(x-\mu_x-\Sigma_{xy}\Sigma_{yy}^{-1}(y-\mu_y)) }_{\bf p(x|y)\text{部分}} \\ &+ \underbrace{ \bf (y-\mu_y)^T\Sigma_{yy}^{-1}(y-\mu_y) }_{\bf p(y)\text{部分}} \end{aligned}$$

从而得到：

$$\bf p(x | y) = \mathcal N\left( \mu_x + \Sigma_{xy}\Sigma_{yy}^{-1}( y - \mu_y), \quad \Sigma_{xx} - \Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx} \right)$$

这也证明了，$\begin{bmatrix} \bf\Omega_{xx}&\bf\Omega_{xy}\\\bf\Omega_{yx}&\bf\Omega_{yy} \end{bmatrix}$中，$\bf\Omega_{xx}$是$\bf p(x|y)$的信息矩阵，相应地，$\bf\Omega_{xx}$是$\bf p(y|x)$的信息矩阵。

为了边缘化$\bf y$以求$\bf p(x)$，再使用上文矩阵求逆引理得到$\bf\Omega_{xx}$的另一个表达形式，以及其他分块矩阵的表达形式：

$$\begin{aligned} \bf \Omega_{xx} &= \bf \Sigma_{xx}^{-1} + \Sigma_{xx}^{-1}\Sigma_{xy}\underline{\left( \Sigma_{yy} - \Sigma_{yx}\Sigma_{xx}^{-1}\Sigma_{xy} \right)^{-1}}\Sigma_{yx}\Sigma_{xx}^{-1} \\ \bf \Omega_{xy} &= \bf -\Sigma_{xx}^{-1}\Sigma_{xy}\underline{\left( \Sigma_{yy} - \Sigma_{yx}\Sigma_{xx}^{-1}\Sigma_{xy} \right)^{-1}} \\ \bf \Omega_{yx} &= \bf -\underline{\left( \Sigma_{yy} - \Sigma_{yx}\Sigma_{xx}^{-1}\Sigma_{xy} \right)^{-1}}\Sigma_{yx}\Sigma_{xx}^{-1} \\ \bf \Omega_{yy} &= \bf \underline{\left( \Sigma_{yy} - \Sigma_{yx}\Sigma_{xx}^{-1}\Sigma_{xy} \right)^{-1}} \end{aligned}$$

注意上面划横线的部分都是一样的。然后我们可以容易地验证：$\bf \Omega_{xx} - \Omega_{xy}\Omega_{yy}^{-1}\Omega_{yx} = \Sigma_{xx}^{-1}$，因为$\bf \Omega_{xy}\Omega_{yy}^{-1}\Omega_{yx}$恰好把$\bf\Omega_{xx}$的后面一坨消掉了。因此

$$\begin{aligned} \bf\Omega_x &= \bf\Sigma_{xx}^{-1} \\ &= \bf \Omega_{xx} - \Omega_{xy}\Omega_{yy}^{-1}\Omega_{yx} \end{aligned}$$

也就是说对信息矩阵使用舒尔补求的是边缘概率，而直接扔掉求的是条件概率。

高斯牛顿法的边缘化

我们知道海森矩阵就是信息矩阵，于是如果我们想要扔掉一些变量，就用舒尔补进行边缘化。直接抠掉信息矩阵中对应行列的话，相当于把扔掉的变量作为条件传递下去了；而条件概率的方差总是要小于等于非条件概率，那么就会导致对剩下变量的估计“过于乐观”。因此我们应该选择边缘概率而不是条件概率。

下面我们推导边缘化之后的信息矩阵和信息向量。边缘化之前：

$$\begin{aligned} \bf x &= \begin{bmatrix} \bf \Delta x_B \\ \bf \Delta x_C \end{bmatrix}, \\ \bf b &= \begin{bmatrix} \bf b_B \\ \bf b_C \end{bmatrix}, \\ \bf H &= \begin{bmatrix} \bf B & \bf E \\ \bf E^T & \bf C \end{bmatrix} \\ &= \begin{bmatrix} \bf I & \bf EC^{-1} \\ & \bf I \end{bmatrix} \underbrace { \begin{bmatrix} \bf B-EC^{-1}E^T & \\ & \bf C \end{bmatrix} \begin{bmatrix} \bf I & \\ \bf C^{-1}E^T & \bf I \end{bmatrix} }\\ &= \begin{bmatrix} \bf I & \bf EC^{-1} \\ & \bf I \end{bmatrix} \begin{bmatrix} \bf B-EC^{-1}E^T & \\ \bf E^T & \bf C \end{bmatrix} \end{aligned}$$

于是高斯牛顿法要求的方程如下：

$$\begin{aligned} \bf Hx &= \bf b \\ \bf \begin{bmatrix} \bf I & \bf EC^{-1} \\ & \bf I \end{bmatrix} \begin{bmatrix} \bf B-EC^{-1}E^T & \\ \bf E^T & \bf C \end{bmatrix} x &= \bf b \\ \bf \begin{bmatrix} \bf B-EC^{-1}E^T & \\ \bf E^T & \bf C \end{bmatrix} x &= \bf \begin{bmatrix} \bf I & \bf -EC^{-1} \\ & \bf I \end{bmatrix} b \\ \bf \begin{bmatrix} \bf B-EC^{-1}E^T & \\ \bf E^T & \bf C \end{bmatrix} \begin{bmatrix} \bf \Delta x_B \\ \bf \Delta x_C \end{bmatrix} &= \bf \begin{bmatrix} \bf I & \bf -EC^{-1} \\ & \bf I \end{bmatrix} \begin{bmatrix} \bf b_B \\ \bf b_C \end{bmatrix} \\ \bf \begin{bmatrix} \bf B-EC^{-1}E^T & \\ \bf E^T & \bf C \end{bmatrix} \begin{bmatrix} \bf \Delta x_B \\ \bf \Delta x_C \end{bmatrix} &= \begin{bmatrix} \bf b_B - EC^{-1} b_C\\ \bf b_C \end{bmatrix} \\ \Downarrow \Downarrow \Downarrow\\ \end{aligned}$$ $$\begin{cases} \bf \underbrace{(B-EC^{-1}E^T)}_{\bar H}\Delta x_B &= \bf \underbrace{b_B - EC^{-1} b_C}_{\bar b} \\ \bf E^T\Delta x_B + C\Delta x_C &= \bf b_C \end{cases}$$

于是将$\bf\Delta x_C$边缘化后，$\bf Hx=b$转为$\bf \bar Hx=\bar b$。这个$\bf\Delta x_C$可以代表老旧的状态变量更新量，这意味着被边缘化之后的变量将固定下来不再变化。

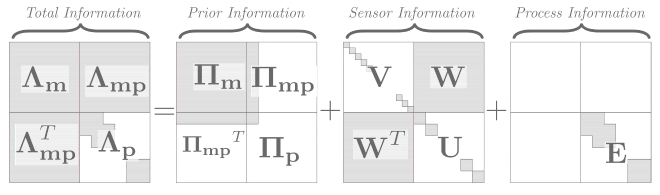
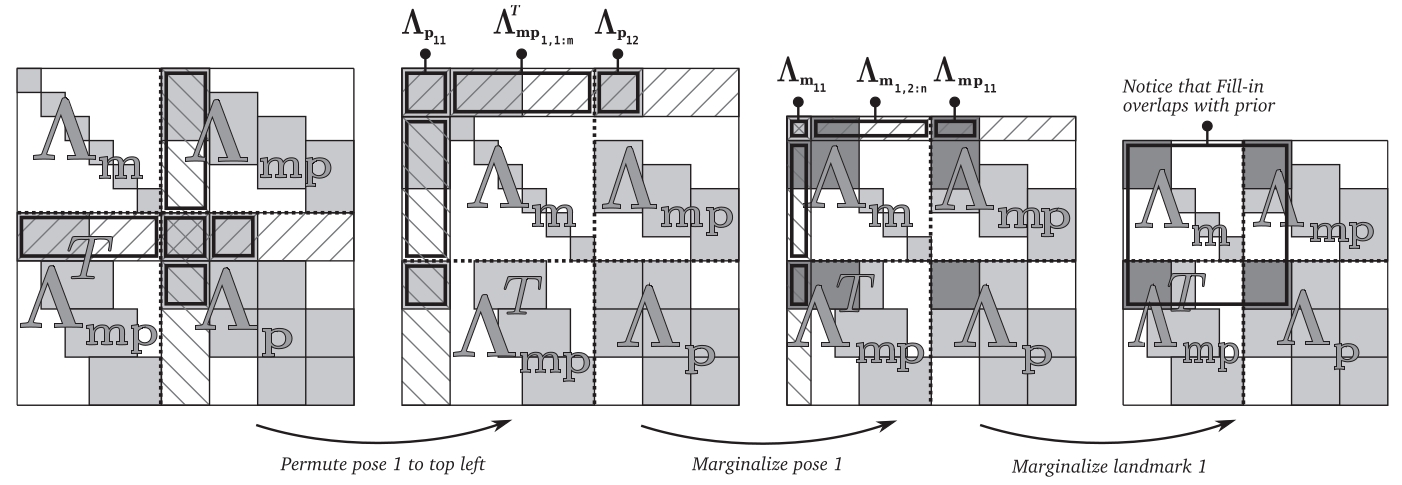
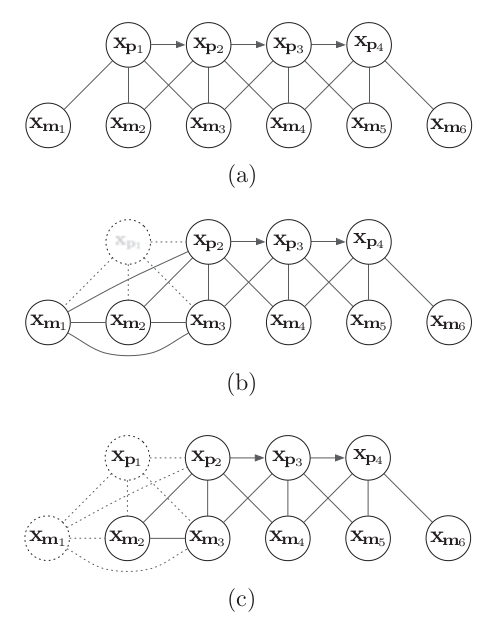
需要注意的是，在边缘化之后信息矩阵引入了先验$\bf -EC^{-1}E^T$，而在边缘化之前这块矩阵可能是对角块矩阵，边缘化之后剩下的这块矩阵就不一定是对角块矩阵了，于是求逆变得比较困难，这种情况被称为“fill-in”：

总信息矩阵=其他的先验+似然（观测）+运动先验

将p1和m1边缘化之后矩阵变小而更加稠密

边缘化过程的因子图：边缘化之后产生了新的边

补充：cholesky分解进行边缘化

对一个对称矩阵可使用Cholesky分解为两个三角矩阵的乘积：$\bf A = LL^T$，这在解方程时候很方便：

$$\begin{aligned} \bf Ax &= \bf b \\ \bf L\underbrace{L^Tx}_{\bf y} &= \bf b \\ & \Downarrow \\ & \begin{cases} \bf Ly &= \bf b \\ \bf L^Tx &= \bf y \end{cases} \end{aligned}$$

因为$\bf L,L^T$是三角矩阵，所以可以由上往下、由下往上地进行消元，先求解$\bf y$，再求解最终的$\bf x$。

如果我们对一个分块矩阵进行Cholesky分解：

$$\begin{bmatrix} \bf B & \bf E \\ \bf E^T & \bf C \end{bmatrix} = \begin{bmatrix} \bf U_{11} & \bf U_{12} \\ & \bf U_{22} \end{bmatrix} \begin{bmatrix} \bf U_{11}^T & \\ \bf U_{12}^T & \bf U_{22}^T \end{bmatrix}$$

其中

$$\begin{aligned} \bf U_{22}U_{22}^T &= \bf C \\ \bf U_{12}U_{22}^T &= \bf E \\ \bf U_{11}U_{11}^T + U_{12}U_{12}^T &= \bf B \end{aligned}$$

因为$\bf B,C$是对角块矩阵，因此很容易求得$\bf U_{11},U_{12},U_{22}$。

如果我们在解高斯牛顿方程时候进行分解：

$$\begin{aligned} \bf Hx &= \bf b \\ \bf \begin{bmatrix} \bf B & \bf E \\ \bf E^T & \bf C \end{bmatrix} \begin{bmatrix} \bf \Delta x_B \\ \bf \Delta x_C \end{bmatrix} &= \begin{bmatrix} \bf b_B \\ \bf b_C \end{bmatrix} \\ \bf \underbrace{\begin{bmatrix} \bf U_{11} & \bf U_{12} \\ & \bf U_{22} \end{bmatrix}}_\text{移到右边} \begin{bmatrix} \bf U_{11}^T & \\ \bf U_{12}^T & \bf U_{22}^T \end{bmatrix} \begin{bmatrix} \bf \Delta x_B \\ \bf \Delta x_C \end{bmatrix} &= \begin{bmatrix} \bf b_B \\ \bf b_C \end{bmatrix} \\ \bf \begin{bmatrix} \bf U_{11}^T & \\ \bf U_{12}^T & \bf U_{22}^T \end{bmatrix} \begin{bmatrix} \bf \Delta x_B \\ \bf \Delta x_C \end{bmatrix} &= \begin{bmatrix} \bf U_{11}^{-1} & \bf -U_{11}^{-1}U_{12}U_{22}^{-1} \\ & \bf U_{22}^{-1} \end{bmatrix} \begin{bmatrix} \bf b_B \\ \bf b_C \end{bmatrix} \\ \bf \begin{bmatrix} \bf U_{11}^T & \\ \bf U_{12}^T & \bf U_{22}^T \end{bmatrix} \begin{bmatrix} \bf \Delta x_B \\ \bf \Delta x_C \end{bmatrix} &= \begin{bmatrix} \bf U_{11}^{-1}(b_B - U_{12}U_{22}^{-1}b_C) \\ \bf U_{22}^{-1}b_C \end{bmatrix} \end{aligned}$$

同样的，我们只取第一行的方程。其实这个方程本质上与舒尔补边缘化之后的方程一样，只不过提早将舒尔补之后的海森矩阵进行Cholesky分解了：

$$\begin{aligned} \bf U_{11}^T\Delta x_B &= \bf U_{11}^{-1}(b_B - U_{12}U_{22}^{-1}b_C) \\ \bf U_{11}U_{11}^T\Delta x_B &= \bf b_B - U_{12}U_{22}^{-1}b_C \\ \end{aligned}$$

由Cholesky分解整理得到：

$$\begin{cases} \bf U_{12} &= \bf EU_{22}^{-T} \\ \bf U_{12}U_{12}^T &= \bf EU_{22}^{-T}U_{22}^{-1}E^T \\ \bf U_{22} &= \bf CU_{22}^{-T} \\ \bf U_{22}^{-1} &= \bf U_{22}^TC^{-1} \\ \end{cases}$$

代入上式：

$$\begin{aligned} \bf U_{11}U_{11}^T &= \bf B - U_{12}U_{12}^T \\ &= \bf B - E\underbrace{U_{22}^{-T}U_{22}^{-1}}_{C^{-1}}E^T \\ &= \bf B - EC^{-1}E^T \\ \bf b_B - U_{12}U_{22}^{-1}b_C &= \bf b_B - E\underbrace{U_{22}^{-T}U_{22}^T}_{I}C^{-1}b_C \\ &= \bf b_B - EC^{-1}b_C \\ \Downarrow \\ \bf \underbrace{(B-EC^{-1}E^T)}_{\bar H}\Delta x_B &= \bf \underbrace{b_B - EC^{-1} b_C}_{\bar b} \end{aligned}$$

得到与舒尔补一样的结果，只不过提早将舒尔补之后的海森矩阵进行Cholesky分解了：$\bf U_{11}U_{11}^T = B - EC^{-1}E^T$；实际上因为边缘化之后的海森矩阵变得稠密了，但毕竟还是一个对称矩阵，此时解方程往往也是通过分解来解的。

不同窗口大小的最大后验估计法

下面要讨论卡尔曼滤波（KF）、扩展KF（EKF）、迭代EKF（IEKF）、滑动窗口滤波（SWF）、光束平差法（bundle adjustment，BA）之间的关系。IEKF、SWF、BA都是最大后验估计的方法，只不过窗口大小不同。

上一篇博客比较详细地推导了卡尔曼滤波器的5个公式如下，用到的方法是，先求$\bf p(x)$先验以及$\bf p(x,y)$联合概率，从而得到$\bf p(x|y)$后验概率。求先验的时候总结出预测两个式子，求后验时候总结出更新两个式子，而后验中重复性高的式子总结为卡尔曼增益：

$$\begin{aligned} 系统建模：& \begin{cases} \bf x_k = A_k x_{k-1} + \overbrace{w_k}^\text{输入} + \overbrace{u_k}^{\text{噪声方差}Q_k} \\ \bf y_k = C_k x_{k} + \underbrace{v_k}_{\text{噪声方差}R_k} \end{cases} \\ \\ 预测(先验)：& \begin{cases} \bf\check{x}_k &= \bf A_k\hat{x}_{k-1} + w_k \\ \bf\check{P}_k &= \bf A_k\hat{P}_{k-1} A_k^T + Q_k \end{cases} \\ 卡尔曼增益：& \begin{cases} \bf K_k &= \bf\check{P}_k C_k^T(C_k\check{P}_kC_k^T + R_k)^{-1} \end{cases} \\ 更新(后验)：& \begin{cases} \bf\hat{x}_k &= \bf \check{x}_k + K_k(y_k - C_k\check{x}_k) \\ \bf\hat{P}_k &= \bf (I - K_kC_k)\check{P}_k \end{cases} \end{aligned}$$

线性情况的卡尔曼滤波(KF)扩展到非线性情况下就是扩展卡尔曼滤波(EKF)。具体方法是，将观测方程进行一阶泰勒展开从而线性化

$$\begin{aligned} 系统建模：& \begin{cases} \bf x_k &= \bf f(x_{k-1}) + \overbrace{w_k}^\text{输入} + \overbrace{u_k}^{\text{噪声方差}Q_k} \\ & \approx \bf f(\bar x_{k-1}) + F_k \Delta x_{k} + w_k + u_k \\ \bf y_k &= \bf g(x_{k}) + \underbrace{v_k}_{\text{噪声方差}R_k} \\ & \approx \bf g(\bar x_{k}) + G_k \Delta x_{k} + v_k \end{cases} \\ \\ 预测(先验)：& \begin{cases} \bf\check{x}_k &= \bf f(\hat{x}_{k-1}) + w_k \\ \bf\check{P}_k &= \bf F_k\hat{P}_{k-1} F_k^T + Q_k \end{cases} \\ 卡尔曼增益：& \begin{cases} \bf K_k &= \bf\check{P}_k G_k^T(G_k\check{P}_kG_k^T + R_k)^{-1} \end{cases} \\ 更新(后验)：& \begin{cases} \bf\hat{x}_k &= \bf \check{x}_k + K_k(y_k - G_k\check{x}_k) \\ \bf\hat{P}_k &= \bf (I - K_kG_k)\check{P}_k \end{cases} \end{aligned}$$

在非线性情况下，EKF仅通过一次线性近似去估计后验状态，这在很多情况下是不够的；很自然地我们想到对它进行多轮迭代，每次估计$\bf \hat x_k$都进行多次EKF，每次都对运动方程和观测方程线性化得到一系列$\bf F_{k,i}$和$\bf G_{k,i}$，进而得到一系列$\bf x_{k,i}$不断收敛至真实值。这就是IEKF，显然这是比单纯EKF要好，但是计算量更大。

下面我们讨论滑动窗口，即建立一个长度为$m$的窗口，储存$\bf [ x_{k-m}, \dots, x_{k-1}]$共m个状态值。当需要估计新的状态$\bf x_k$时，将其加入窗口，然后将最老的状态$\bf x_{k-m}$边缘化出去。这也被称为局部BA。显然所谓全局BA就是窗口达到最大，包含了所有需要估计的状态的bundle adjustment。

窗口中的变量可以写在一起：$\bf X_k = [ x_{k-m}, \dots, x_{k-1} ]$，$\bf Y_k = [ y_{k-m}, \dots, y_{k-1} ]$，从而要求的是$\bf p(X_k|Y_k)$。这可以用迭代卡尔曼滤波器的方法，也可以用高斯牛顿法；这两种方法本质上是一样的，讨论如下：

我们首先仅考虑观测方程，也就是没有运动方程，也就是没有先验，也就是先验的协方差矩阵$\bf \check P_k = \infty$。为了统一，我们用$\bf J_k$而不是$\bf G_k$来表示观测方程的一阶导数，即雅可比矩阵；同时观测方程的方差写为$\bf W$而不是$\bf R_k$。

IEKF中，卡尔曼增益利用矩阵求逆引理改写为以下形式：

$$\begin{aligned} \bf K_k &= \bf\check{P}_k J_k^T(J_k\check{P}_kJ_k^T + W)^{-1} \\ &= \bf (\underbrace{\check{P}_k^{-1}}_{\infty^{-1}=0} + J_k^TW^{-1}J_k)^{-1}J_k^TW^{-1} \\ &= \bf (J_k^TW^{-1}J_k)^{-1}J_k^TW^{-1} \end{aligned}$$

代入后验更新中：

$$\begin{aligned} \bf\hat{x}_k &= \bf \underbrace{\check{x}_k}_{\bf \hat x_{k-1}} + \underbrace{K_k \overbrace{(y_k - G_k\check{x}_k)}^{\text{估计误差}e_{k-1}}}_{\bf\Delta x} \\ & \Downarrow \\ \bf \Delta x &= \bf (J_k^TW^{-1}J_k)^{-1}J_k^TW^{-1}e_{k-1} \\ & \Downarrow \\ \bf \underbrace{J_k^TW^{-1}J_k}_{\text{海森矩阵}H} \Delta x &= \bf J_k^TW^{-1}e_{k-1} \end{aligned}$$

于是就得到了高斯牛顿法。这正好说明IEKF是窗口长度为1的局部BA。

如果我们考虑先验的话，海森矩阵就会加上先验：

$$\begin{aligned} \bf K_k &= \bf\check{P}_k J_k^T(J_k\check{P}_kJ_k^T + W)^{-1} \\ &= \bf (\underbrace{\check{P}_k^{-1}}_\text{先验信息矩阵} + J_k^TW^{-1}J_k)^{-1}J_k^TW^{-1} \\ \\ \bf \Delta x &= \bf (\check{P}_k^{-1} + J_k^TW^{-1}J_k)^{-1}J_k^TW^{-1}e_{k-1} \\ & \Downarrow \\ \bf \underbrace{(\check{P}_k^{-1} + J_k^TW^{-1}J_k)}_{\text{海森矩阵}H} \Delta x &= \bf J_k^TW^{-1}e_{k-1} \end{aligned}$$

这个先验，可以来自于真的环境的先验，也可以来自于边缘化老的与窗口内的状态变量有关联的变量，也就是舒尔补边缘化海森矩阵中的$\bf -EC^{-1}E^T$部分。

虽然迭代卡尔曼滤波的方法和高斯牛顿法本质上一样，但是卡尔曼滤波器关注的是协方差矩阵，这并不那么直接可以得到的，会引入更多的矩阵求逆运算；而高斯牛顿法使用的信息矩阵则可以直接通过观测方程的导数得到，如果观测方程是解析的那就更直接了。因此在大规模的情况下，后者要比前者更有优越性。应该说，卡尔曼滤波关注均值和协方差矩阵，信息滤波关注信息向量和信息矩阵，而最小二乘法或高斯牛顿法则关注均值和信息矩阵；后者选择的两方面都恰好容易直接获得，而且具有符合现实的含义。

滑动窗口边缘化的弊端与FEJ

关于First estimate Jacobian（FEJ）有关于系统能观性的更深刻的讨论，但这里仅做感性的讨论。

因为每做一次估计，都要迭代多次，计算多个海森矩阵以及$\bf \Delta x$，每次都在不同的$\bf x+\Delta x$处对观测方程求导。对于已经边缘化了的变量，它们不再更新，相当于它们的线性化点固定住了；但是如果我们却继续更新窗口中的点，在整个系统的角度上讲就是在不同的点上做了线性化，然后会导致系统的零空间降维，使得我们获得“过于乐观”的解，于是可能会慢慢地破坏整个系统。。

例子

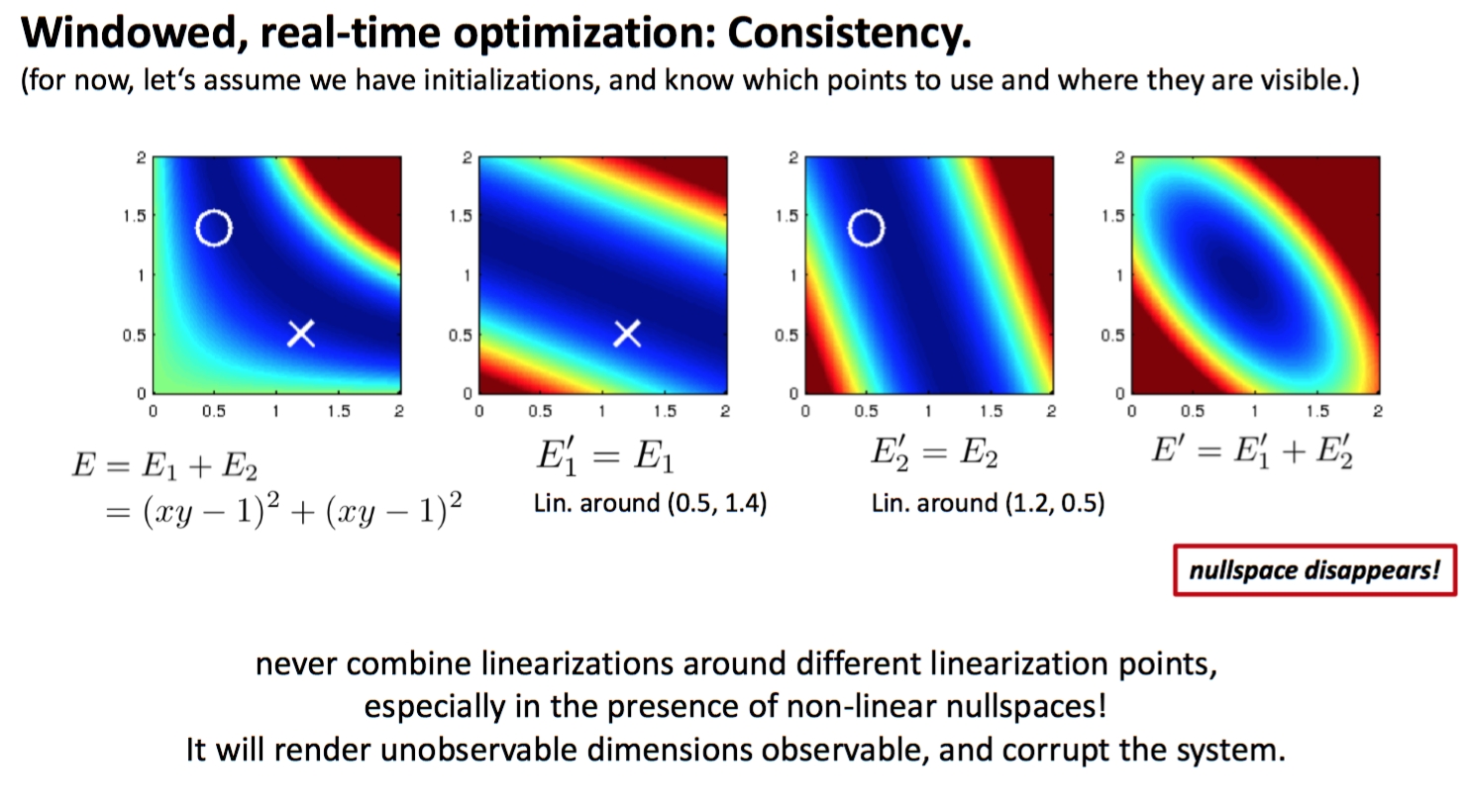
为了避免系统在边缘化前后在不同点上做线性化，就需要保持雅可比矩阵在随后的迭代中不变，也就是只在边缘化时候算一次雅可比，随后就不改变雅可比了，即所谓的“first estimate Jacobian”。DSO等基于滑动窗口的视觉里程计中就是这样做的。这样做显然会降低估计的精度：因为迭代时候它只往同一个方向去搜索，不过它好处是保持了系统零空间维度，保证它的“一致性”（consistency）从而让系统更稳定，而且降低了计算量。

FEJ的做法其实跟所谓forwards compositional法求解图像对齐问题是一样的，下面根据Lucas-Kanade 20 Years on，选取其中几种方法进行介绍。

光流、仿射变换、三维点重投影等操作，都是求两帧图片之间的关系，将某张图T上的像素点经过各自的方法映射到另一张图I上。这些算法可以统一为一类：图像对齐（image alignment），图像对齐用到的映射被称为wrap，它是一个2d到2d的映射：

$$\bf W(\underbrace{x}_\text{像素坐标}, \underbrace{p}_\text{不同算法的参数})$$

例如，如果求的是光流的话，那么wrap可以这样定义：

$$\begin{aligned} \bf W(x,p) &= \bf W(\begin{bmatrix}u\\v\end{bmatrix}, \begin{bmatrix}I_u\\I_v\end{bmatrix}) \\ &= \begin{bmatrix} u+I_u \\ v+I_v \end{bmatrix} \end{aligned}$$

对于三维点重投影的情况，wrap就是将参考帧上的特征点投影到当前帧上的函数。

$$\bf W(x,p) = \pi ( exp(\xi) \pi^{-1}(x, d_x))$$

图像对齐要求的问题是wrap中的参数$\bf p$，对于光流，就是光流向量$\begin{bmatrix}I_u\\I_v\end{bmatrix}$，对于三维点重投影，就是这个点的深度$d_x$和相机之间的相对位移$\xi$。

图像对齐：FA

forwards additive就是最传统的图像对齐方式，它最小化像素的光度差：

$$\bf p = \arg \min_p \sum_x \left[I(W(x,p+\Delta p)) - T(x)\right]^2$$

误差项进行一阶泰勒展开：

$$\bf I(W(x,p+\Delta p)) - T(x) \approx I(W(x,p)) + \underbrace{ \overbrace{\frac{\partial I(u)}{\partial u}}^\text{图像梯度} \overbrace{\frac{\partial W(x,p)}{\partial p}}^\text{W在p处的导数} }_\text{雅可比矩阵} \Delta p - T(x)$$

然后按照上文介绍的高斯牛顿法进行迭代优化，得到$\bf p$。

图像对齐：FC

FA法需要在每次迭代时候重新算一次整个雅可比矩阵，效率并不那么高。而forwards compositional法则采取了另一个角度：先对I做一次小wrap，再在小wrap的基础上做一次大wrap：

$$\bf p = \arg \min_p \sum_x \left[I(W(W(x,\Delta p)),p) - T(x)\right]^2$$ $$\begin{aligned} \bf I(W(W(x,\Delta p),p)) - T(x) & \approx \bf \underbrace{ I(W(\overbrace{W(x,0)}^\text{单位wrap，即x},p)) }_\text{在p=0处进行泰勒展开} + \underbrace{ \overbrace{\frac{\partial I(u)}{\partial u}}^\text{I上的图像梯度} \overbrace{\frac{\partial W(x,p)}{\partial x}}^\text{W对x} }_\text{小wrap之后的图像梯度} \overbrace{\frac{\partial W(x,p)}{\partial p}}^\text{W在p=0处的导数} \Delta p \\ &\quad \bf - \quad T(x) \\ &= \bf I(W(x,p)) + \underbrace{ \frac{\partial I}{\partial W} \frac{\partial W}{\partial p} }_\text{雅可比矩阵} \Delta p - T(x) \end{aligned}$$

可以看到在雅可比矩阵中$\bf \frac{\partial W}{\partial p}$是$\bf p=0$处的导数，不用随着$\bf p$更新而更新，这也顺便降低了一些计算量。当然最大的计算量是海森矩阵的求逆，而因为有$\bf \frac{\partial I}{\partial W}$，海森矩阵并不固定。

而这种方法也被用于所谓FEJ中——海森矩阵与当前的$\bf p$无关，从而就避免了在不同的$\bf p$点上对系统线性化的不一致性。

图像对齐：IC

补充inverse compositional法。与FC法不同，IC法将参考图像和目标图像的地位改变了一下，采取这种策略：将I做一次大wrap，将T做一次小wrap，将这二者进行对齐：

$$\bf p = \arg \min_p \sum_x \left[T(W(x,\Delta p)) - I(W(x,p))\right]^2$$ $$\begin{aligned} \bf T(W(x,\Delta p)) - I(W(x,p)) & \approx \bf \underbrace{ T(\overbrace{ W(x,0) }^\text{单位wrap即x}) }_\text{在p=0处泰勒展开} + \overbrace{ \frac{\partial T(u)}{\partial u} }^\text{T上的梯度} \overbrace{ \frac{\partial W(x,p)}{\partial p} }^\text{W在p=0处的导数} \Delta p - I(W(x,p)) \\ &= \bf T(x) + \underbrace{ \frac{\partial T}{\partial u} \frac{\partial W}{\partial p} }_\text{雅可比矩阵} \Delta p - I(W(x,p)) \end{aligned}$$

这时我们可以看到，雅可比矩阵的两个乘数项都与$\bf p$无关，不用随着$\bf p$更新而更新，从而海森矩阵是固定的，海森矩阵的逆也是固定的，进而大大降低了计算量。这也是SVO采用的方法。

总结

• 求高斯分布的后验分布的均值会引出最小二乘法
• 高斯牛顿方程的海森矩阵就是后验分布的信息矩阵，方程右手边的向量就是其信息向量
• 直接抠出协方差矩阵对应变量的子矩阵得到其边缘分布，做舒尔补则得到其条件分布
• 直接抠出信息矩阵对应变量的子矩阵得到的是其条件分布，做舒尔补则得到的是其边缘分布
• IEKF相当于窗口长度为1的滑动窗口方法，窗口长度扩展到所有变量则等价于全局BA
• 滑动窗口边缘化变量时不再更新老变量从而导致系统的线性化点不同，FEJ只使用0点的雅可比从而保证一致性

参考资料

• 机器人学中的状态估计
• G. Sibley, L. Matthies, and G. Sukhatme. Sliding window filterwith application to planetary landing.JFR, 27(5):587–608, 2010.
• S. Baker, and I. Matthews, “Lucas-Kanade 20 Years on: A Unifying Framework: Part 1,” Int’l J. Computer Vision, vol. 56, no. 3, pp. 221-255, 2004.